
Next, we need to calculate the variance, which is the average of the squared differences between each data point and the mean. We do this by adding up all of the weights and dividing by the total number of apples: To calculate the standard deviation of this data set, we first need to find the mean, or average, weight of the apples. Let’s say we have a set of data consisting of the weights of ten apples, in grams: If the standard deviation is calculated for a sample of the product, using the Population Standard Deviation formula could underestimate the amount of variation in weight, leading to incorrect conclusions about the process and potential improvements. Failing to use the correct formula could lead to inaccurate conclusions and decisions.įor example, if a Six Sigma project is focused on improving the quality of a product, the standard deviation of the product’s weight could be calculated to identify the amount of variation in weight. In that case, it is important to use the Sample Standard Deviation formula to account for the fact that the sample may not perfectly represent the population as a whole. Suppose the standard deviation is being calculated for a sample. In a Six Sigma project, it is vital to understand whether the standard deviation is being calculated for the entire population or just a population sample. To achieve this goal, Six Sigma practitioners use statistical tools and methods, including standard deviation, to identify and reduce variability in a process. So why is understanding the difference between Population Standard Deviation and Sample Standard Deviation important for a Six Sigma project? Six Sigma is a data-driven approach to quality improvement that seeks to reduce defects and errors in a process to 3.4 defects per million opportunities. Sample Standard Deviation, on the other hand, uses a slightly different formula that divides the sum of the squared differences between each data point and the sample mean by the sample size minus one. Population Standard Deviation uses a formula that divides the sum of the squared differences between each data point, and the population mean by the total number of data points in the population. The main difference between Population Standard Deviation and Sample Standard Deviation is the formula used to calculate them.
On the other hand, Sample Standard Deviation is used to measure the standard deviation of a sample, which is a smaller subset of the population being studied. Population Standard Deviation measures the standard deviation of a population, which is the entire group of people, objects, or events being studied. Two common standard deviation types are Population Standard Deviation and Sample Standard Deviation. It is an important tool used in statistical analysis to measure how spread out the data is. In statistics, standard deviation measures a dataset’s variation or dispersion.
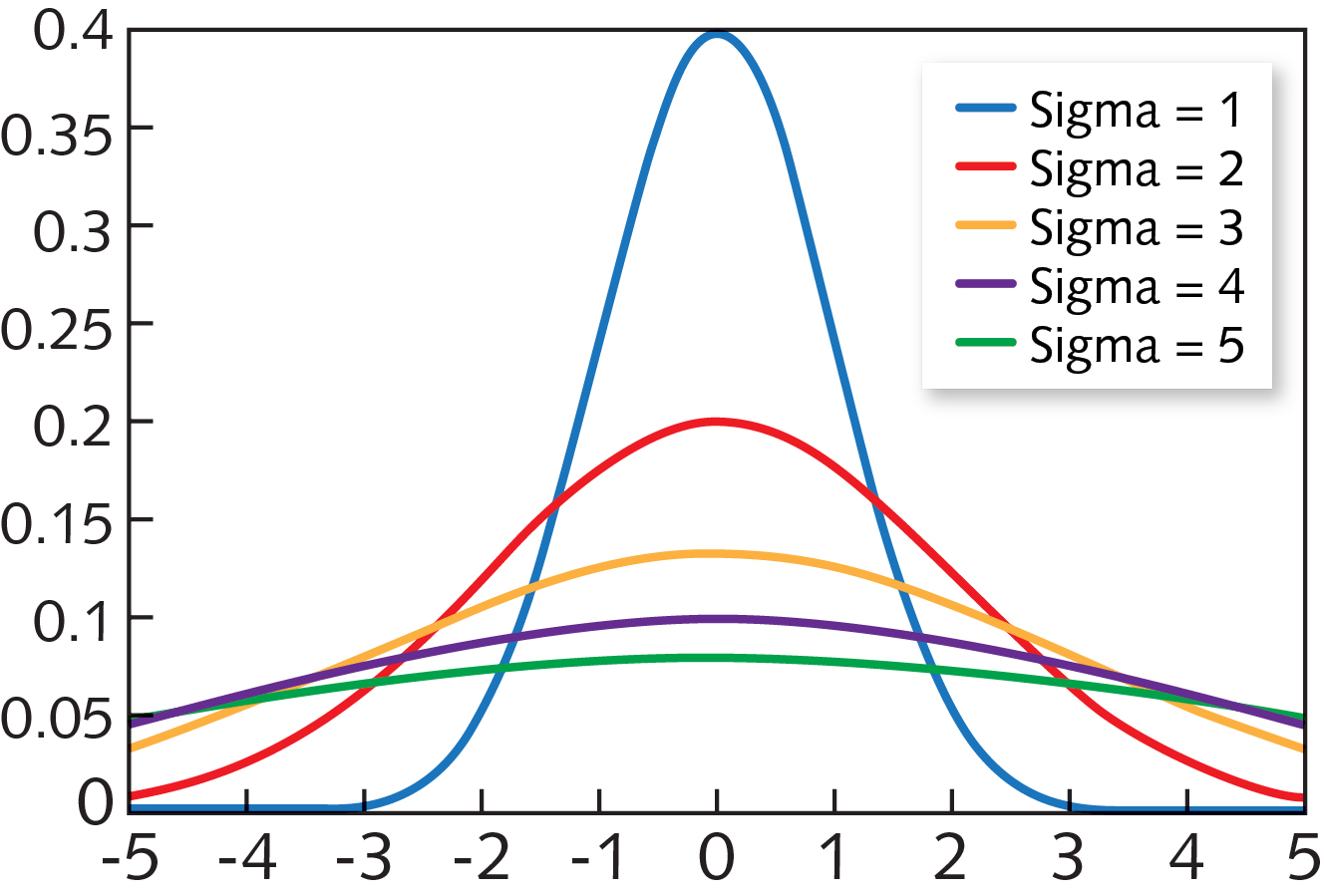
The normal distribution is also known as the Gaussian distribution, after the mathematician Carl Friedrich Gauss, who developed the theory of least squares, which is used to fit a normal distribution to a set of data.(3) Gauss’s work laid the foundation for the field of statistics and has significantly impacted how we analyze data. This is in contrast to a discrete distribution, in which only a finite number of possible values exist. One of the key characteristics of the normal distribution is that it is continuous, meaning that there is an infinite number of possible values between any two points on the curve. The curve is shaped like a bell, hence the name “bell curve.” In a normal distribution, about 68% of the data falls within one standard deviation of the mean, 95% within two standard deviations, and 99.7% within three standard deviations. The normal distribution is defined by a curve, with the majority of the data points clustered around the mean and fewer data points towards the extremes. It is also the basis for statistical tests such as the t-test and z-test, which are used to compare means and determine the likelihood that a result is due to chance. The mean for the standard normal distribution is zero, and the standard deviation is one.The normal distribution is important because it is used to model many real-world phenomena, such as IQ scores, height, and weight. For example, if the mean of a normal distribution is five and the standard deviation is two, the value 11 is three standard deviations above (or to the right of) the mean. A z-score is measured in units of the standard deviation.

The standard normal distribution is a normal distribution of standardized values called z-scores. Recognize the standard normal probability distribution and apply it appropriately.


 0 kommentar(er)
0 kommentar(er)
